Funciones Matemáticas

Una función es una relación establecida entre dos variables que asocia a cada valor de la primera variable (variable independiente x), un único valor de la segunda variable (variable dependiente y). Esta relación se representa mediante y = f(x) Las funciones se pueden determinar de varias formas:  Mediante una tabla de valores .  Mediante su expresión analítica.   Mediante su gráfica.  Si una función viene determinada por una fórmula, para obtener el dominio de la función debemos tener en cuenta, las restricciones que tienen las operaciones algebraicas con números reales:   No está permitido dividir ningún número real por 0.   Se permiten radicales de índice par sólo si el radicando es mayor o igual a 0.   Se permiten logaritmos sólo si el argumento es mayor estricto que u Otros motivos:   Por el contexto del problema del cual se ha extraído la función.   Por voluntad o interés de quien propone la función Dada una función   a cada elemento   del dominio le corresponde

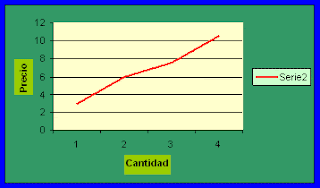
Las funciones son de mucho valor y utilidad para resolver problemas de la vida diaria, problemas de finanzas, economía, de estadística, de ingeniería, de medicina, de química, física, etc. Y de cualquier otra área social donde haya que relacionar variables. Un ejemplo común es cuando se va al mercado o a cualquier centro comercio donde siempre se relacionan un conjunto de determinados objetos con el costo expresado en pesos para saber cuanto podemos comprar. Si lo llevamos al plano, podemos escribir esta correspondencia en una ecuación de función “x” como la cantidad y el precio como “y”, es decir la cantidad en el eje de las abscisas y el precio en el eje de las ordenadas y así expresarlo en un gráfico como el siguiente, donde se expresa que: un Kilogramo de manzana cuesta $3, Entonces: un Kilogramo y medio de manzana cuesta $4,50 etc. En la gráfica lo podemos expresar así: En este caso las funciones, siempre tiene su aplicación en la vida c

La inyectividad, sobreyectividad y biyectividad dan información acerca de como se relacionan los elementos del conjunto inicial X con el conjunto final Y. Cabe recordar que una función f es una relación que asigna a los elementos de un primer conjunto (conjunto inicial X) un elemento de un segundo conjunto (conjunto final Y). Función Inyectiva  Función inyectiva La función f es inyectiva si cada elemento del conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde. Es decir, no pueden haber más de un valor de X que tenga la misma imagen Y. Reciben también el nombre de funciones “uno a uno”. No siempre todos los elementos del conjunto final Y deben corresponderse con alguno del conjunto inicial X. En términos matemáticos, una función f será inyectiva si dados dos puntos xa y xb: Dicho de otra manera: una función es inyectiva si se cumple que a valores de su dominio x0 ≠ x1 ⇒ f(x0) ≠ f(x1). Una comprobación gráfica de la inyectiv

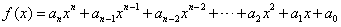
Función polinomial Una función polinomial es una función en que f ( x ) es un polinomio en x . Una función polinomial de grado n es escrita como   POLINOMIALES DE GRADO BAJO NOMBRE FORMA GRADO Función constante f  (  x  ) =  a 0 Función lineal f  (  x  ) =  ax + b, a  ≠ 0 1 Función cuadrática f  (  x  ) =  ax  2  +  bx + c  ,  a  ≠ 0 2 Función cúbica f  (  x  ) =  ax  3  +  bx  2  +  cx  +  d, a  ≠ 0 3 Función constante Una función constante f es una función tal que la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x). En términos matemáticos, la función f es constante si para cualquier par de puntos x1 y x2 del dominio tales que x1<x2, se cumple que f(x1) = f(x2). La gráfica de una función constante es una recta paralela al eje de abscisas X. También se puede definir

Una función es racional si es el cociente de dos polinomios: siendo el grado del polinomio    Q(x)    distinto de 0. Las características generales de las funciones racionales son: 1) El dominio de las funciones racionales son los números reales menos las raíces del denominador,        es decir:      dominio funcion racional 2) Son discontinuas en los valores de    x    que son raíces del denominador. 3) Tienen asíntotas verticales en cada raíz del denominador que no lo sea del numerador, y pueden tener asíntotas horizontales y oblicuas. Por ejemplo en una función f (x ) = 1 / x – 2, el dominio es toda x excepto x =2. Cuando se hace la gráfica de una función racional es importante saber: Qué se puede decir de los valores de la función cuando x se acerca a un cero del denominador? Qué se puede decir de los valores de la función cuando x es grande y positiva o negativa? Asíntota vertical La recta x = a es una asíntota vertical de la gráfica de una función