Funciones inyectivas, sobreyectivas, biyectivas, identidad y constante

La inyectividad, sobreyectividad y biyectividad dan información acerca de como se relacionan los elementos del conjunto inicial X con el conjunto final Y.

Cabe recordar que una función f es una relación que asigna a los elementos de un primer conjunto (conjunto inicial X) un elemento de un segundo conjunto (conjunto final Y).

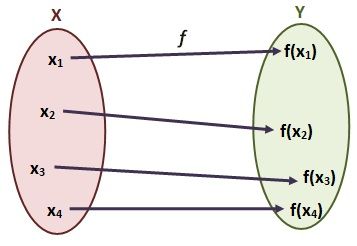
Función Inyectiva 

Función inyectiva

La función f es inyectiva si cada elemento del conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde. Es decir, no pueden haber más de un valor de X que tenga la misma imagen Y. Reciben también el nombre de funciones “uno a uno”.

No siempre todos los elementos del conjunto final Y deben corresponderse con alguno del conjunto inicial X.

En términos matemáticos, una función f será inyectiva si dados dos puntos xa y xb:

Dicho de otra manera: una función es inyectiva si se cumple que a valores de su dominio x0 ≠ x1 ⇒ f(x0) ≠ f(x1).

Una comprobación gráfica de la inyectividad de una función es cuando cualquier recta paralela al eje X corta a la misma, como máximo, en un punto

La función f(x) = 2x+1 , con los elementos de su dominio restringidos a los números reales positivos, es inyectiva.

Veamos que se cumple la condición de inyectividad:

En efecto, si xa y xb tienen la misma imagen, necesariamente deben ser el mismo elemento. Por lo tanto, f es inyectiva.

Veamos la gráfica de otra función:

Esta función no cumple la condición de inyectividad, por lo que no es inyectiva.

Función sobreyectiva

Una función f es sobreyectiva (o suprayectiva) si todo elemento del conjunto final Y tiene al menos un elemento del conjunto inicial X al que le corresponde.

Es decir, una función es sobreyectiva si el recorrido de la función es el conjunto final Y. Dicho de otra manera, una función es sobreyectiva cuando son iguales su codominio y su dominio.

En términos matemáticos, una función f es sobreyectiva si:

Ejemplo de función sobreyectiva

La función en los números reales definida por f(x) = x+1 es sobreyectiva.

Esta función sí que es sobreyectiva. Vamos a verlo demostrando que el recorrido de la función son todos los números reales.

El recorrido de la función es el mismo que el conjunto final Y, por lo que la f es sobreyectiva.

Es decir, que, con la función f(x), todo número real será imagen de, como mínimo, otro número real.

Igualmente, con los mismos argumentos, será sobreyectiva la función:

Función biyectiva

Una función f es biyectiva si es al mismo tiempo inyectiva y sobreyectiva. Es decir, si todo elemento del conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde (condición de función sobreyectiva) y todos los elementos del conjunto inicial X tiene una única imagen en el conjunto final Y (condición de función inyectiva).

Digamos que no puede quedarse ningún elemento en el conjunto final Y solo, sin asociarse con un único elemento del conjunto inicial X.

Teóricamente, una función f es biyectiva si:

Ejemplo de función biyectiva

La función f(x) = 2x definida en los números reales es biyectiva.

Para comprobarlo, veamos que f es inyectiva y sobreyectiva. Empezaremos por la condición de inyectividad:

Se cumple la condición de inyectividad, por lo que ahora nos quedaría demostrar la sobreyectividad. Para ello, tenemos que demostrar que el recorrido de la función son todos los números reales.

La función también es sobreyectiva, por lo que f es biyectiva.

Función identidad 

La función identidad es del tipo:

f(x) = x

Su gráfica es la bisectriz del primer y tercer cuadrante.

Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.

La función identidad también suele denotarse por id.

La pendiente es la inclinación con respecto al eje X (eje de abscisas).
 Al ser ésta positiva (m > 0), la función es creciente.

Que la pendiente de la función identidad sea m = 1 significa que si aumentamos
la x en una unidad,  la y también aumenta en una unidad.

Formará un ángulo de 45° con cualquiera de los ejes.

La identidad id es el elemento neutro en la composición de funciones.
Es decir, cualquier función f compuesta con la identidad es ella misma.