Funciones logarítmicas y exponenciales,Funciones trigonométricas,Software para graficarlas
Funciones logarítmicas
La función logarítmica "básica" es la función, y =
log b x , donde b > 0
y b ≠ 1.
La gráfica de la función logarítmica y = log 10 x se muestra a
continuación.
Observe que la función logarítmica es la inversa de la función exponencial y = b x y tiene las siguientes propiedades.
1. El dominio es el conjunto de
todos los números reales positivos.
2. El rango es el
conjunto de todos los números reales.
(Ya que la función logarítmica es la inversa de la función exponencial, el dominio de la función logarítmica es el rango de la función exponencial y el rango de la función logarítmica es el dominio de la función exponencial)
(Ya que la función logarítmica es la inversa de la función exponencial, el dominio de la función logarítmica es el rango de la función exponencial y el rango de la función logarítmica es el dominio de la función exponencial)
3. La función es
continua y uno-a-uno.
4. El eje de las y es
la asíntota de la gráfica.
5. La gráfica
intersecta al eje de las x en (1, 0). Esto es, la intercepción en x es 1.
La función logarítmica, y = log b x , puede ser
cambiada en k unidades verticalmente y h unidades
horizontalmente con la ecuación y = log b ( x + h )
+ k .
Cambio Vertical
Si k > 0, la gráfica se desplazaría k unidades
hacia arriba.
Si k < 0, la gráfica se desplazaría k unidades
hacia abajo.
Cambio Horizontal
Si h > 0, la gráfica se desplazaría h unidades
a la izquierda.
Si h < 0, la gráfica se desplazaría h unidades
a la derecha.
Función logarítmica natural
El logaritmo con base e es llamado el logaritmo
natural. Se denota por ln x . La función logarítmica
natural, y = ln x es la inversa de la función
exponencial natural de base, y = e x .
La gráfica de la función logarítmica natural y =
ln x se muestra a continuación.
Ejemplo:
Grafique la función y = log 10 (x – 1)
+ 2.
Comience con la gráfica logarítmica básica y =
log b x . Luego cambie la gráfica 1 unidad a
la derecha y 2 unidades hacia arriba.
Funciones Exponenciales
Las funciones exponenciales son
las funciones que tienen la variable
independiente x en el exponente, es decir,
son de la forma:
Las características
generales de las funciones exponenciales son:
1) El dominio de una función exponencial es R.
2) Su recorrido es (0,
+∞) .
3) Son funciones continuas.
4) Como a0 = 1 ,
la función siempre pasa por el punto (0, 1).
La
función corta el eje Y en el punto (0, 1) y
no corta el eje X.
5) Como a1 = a ,
la función siempre pasa por el punto (1, a).
6) Si a >
1 la función es creciente.
Si 0
< a < 1 la función es decreciente.
7) Son siempre concavas.
8) El eje X es una asíntota horizontal.
·
Si a > 1 :
Al elevar un número mayor que 1 a cantidades negativas cada vez más grandes, el valor de la potencia se acerca a cero, por tanto :
Cuando x → - ∞ , entonces a x → 0
Al elevar un número mayor que 1 a cantidades negativas cada vez más grandes, el valor de la potencia se acerca a cero, por tanto :
Cuando x → - ∞ , entonces a x → 0
·
Si 0 < a < 1 :
Ocurre lo contrario que en el caso anterior :
Cuando x → + ∞ , entonces a x → 0
Ocurre lo contrario que en el caso anterior :
Cuando x → + ∞ , entonces a x → 0
Ejemplo de funciones exponenciales:
1)
Dominio:
El dominio de las
funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2)
Recorrido:
El recorrido de las
funciones exponenciales es (0, + ∞)
Im(f) = Im(g) = (0, +
∞) .
3)
Puntos de corte:
f(0) = 20 =
1 , el punto de corte con el eje Y es (0, 1).
g(0) = - 20 =
1 , el punto de corte con el eje Y es (0, 1).
La
funciones f(x) y g(x) no
cortan al eje X.
4)
Crecimiento y decrecimiento:
La
función f(x) es creciente ya
que a > 1 .
La
función g(x) es decreciente ya
que 0 < a < 1 .
5)
Concavidad y convexidad:
Las
funciones f(x) y g(x) son
concavas.
6)
Asíntotas:
Las
funciones f(x) y g(x) tienen
una asintota en el eje X.
7)
Tabla de valores:
| 1 | La función exponencial es la inversa de la logarítmica: y = ex ⇔ x = Ln y |
|---|---|
| 2 | La función y = ex tiene por dominio R y por recorrido y > 0 |
| 3 | La función y = ex es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = ex es cóncava hacia arriba en todo su dominio. |
| 5 |  |
|---|
Ejemplo de funciones exponenciales: f(x) = ex
1)
Dominio:
El dominio de las
funciones exponenciales es R.
Dom(f) = R .
2)
Recorrido:
El recorrido de las
funciones exponenciales es (0, + ∞)
Im(f) = (0, + ∞) .
3)
Puntos de corte:
f(0) = e0 =
1 , el punto de corte con el eje Y es (0, 1).
La
función f(x) no corta al eje X.
4)
Crecimiento y decrecimiento:
5)
Concavidad y convexidad:
Las
función f(x) es concava.
6)
Asíntotas:
Las función f(x) tiene una asintota en
el eje X
7)
Tabla de valores:
Funciones Trigonométricas
las funciones trigonometricas f son aquellas que están
asociadas a una razón trigonométrica.
Las razones trigonométricas de un ángulo α son las obtenidas
entre los tres lados de un triángulo rectángulo. Es decir, las comparaciones
por su cociente de sus tres lados a, b y c.
Existen seis funciones trigonométricas:
Seno
Su abreviatura son sen o sin (del
latín sinus).
La gráfica de la función seno es:
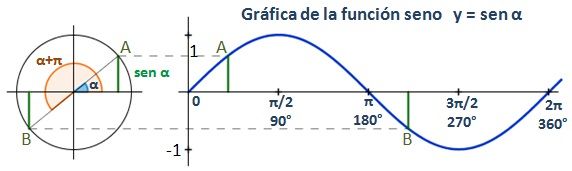
La función del seno es periódica de
período 360º (2π radianes),
por lo que esta sección de la gráfica se repetirá en los diferentes períodos.
- Dominio:
- Codominio:
- Derivada de la función seno:
- Integral de la función seno:
Coseno
El coseno de un ángulo α se
define como la razón entre el cateto contiguo o
cateto adyacente (b) y la hipotenusa (c).
Su abreviatura es cos (del latín cosinus).
La gráfica de la función coseno es:
La función del coseno es periódica de
período 360º (2π radianes).
- Dominio:
- Codominio:
- Derivada de la función coseno:
- Integral de la función coseno:
Tangente
La tangente de un ángulo α es
la razón entre el cateto opuesto (a) y el cateto
contiguo o cateto adyacente (b).
Su abreviatura son tan o tg.
La gráfica de la función tangente es:
La función de la tangente es periódica de
período 180º (π radianes).
- Dominio:
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:
- Derivada de la función tangente:
- Integral de la función tangente:
Cosecante
La cosecante es la razón
trigonométrica inversa del seno, es decir
csc α · sen α=1.
La cosecante del ángulo α de
un triángulo rectángulo se define como la razónentre la hipotenusa (c)
y el cateto opuesto (a).
Su abreviatura es csc o cosec.
La gráfica de la función cosecante es:
La función de la cosecante es periódica de
período 360º (2π radianes).
- Dominio:
(excepto a · π), siendo a un número entero. - Codominio:
- Derivada de la función cosecante:
- Integral de la función cosecante:
Secante
La secante es la razón trigonométrica
inversa del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de
un triángulo rectángulo se define como la razónentre
la hipotenusa (c) y el cateto contiguo o cateto
adyacente (b).
Su abreviatura es sec.
La gráfica de la función secante es:
La función de la secante es periódica de
período 360º (2π radianes).
- Dominio:
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:
- Derivada de la función secante:
- Integral de la función secante:
Cotangente
La cotangente es la razón
trigonométrica inversa de la tangente, por lo tanto
tan α · cot α=1.
La cotangente de un ángulo α de
un triángulo rectángulo se define como la razónentre
el cateto contiguo o cateto adyacente (b) y el cateto
opuesto (a).
Su abreviatura es cot, cotg o cotan.
La gráfica de la función cotangente es:
La función de la cotangente es periódica de
período 180º (π radianes).
- Dominio:
(excepto a · π), siendo a un número entero. - Codominio:
- Derivada de la función cotangente:
- Integral de la función cotangente:
Software para graficar Funciones
Dejamos el enlace directamente, son cantidad de aplicaciones las que se pueden usar para graficar funciones, estas son 4 que nos parecieron bastante buenas
¡Esperamos sean muy útiles para ustedes!
Comentarios
Publicar un comentario