Función polinomial
Función polinomial
Una función polinomial es una
función en que f ( x ) es un polinomio en x .
Una función polinomial de grado n es escrita
como
POLINOMIALES DE GRADO BAJO
|
||
NOMBRE
|
FORMA
|
GRADO
|
Función constante
|
f ( x ) = a
|
0
|
Función lineal
|
f ( x ) = ax + b, a ≠ 0
|
1
|
Función
cuadrática
|
f ( x ) = ax 2 + bx +
c , a ≠ 0
|
2
|
Función cúbica
|
f ( x ) = ax 3 + bx 2 + cx + d, a ≠
0
|
3
|
Función constante
Una función constante f es una función tal que la variable
dependiente y toma el mismo valor a para cualquier elemento del dominio
(variable independiente x).


En términos matemáticos, la función f es constante si para
cualquier par de puntos x1 y x2 del dominio tales que x1<x2, se cumple que
f(x1) = f(x2).

La gráfica de una función constante es una recta paralela al
eje de abscisas X.
También se puede definir una función constante a partir de
la derivada. Una función f será constante si para todo punto x del dominio la
derivada es nula, es decir f ’(x) = 0.
La derivada de la función constante es 0 porque no depende
del valor de la variable independiente x.
Función Lineal
Una función lineal es una función polinómica de grado 1 que
pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones
rectas de la forma:


La m es la pendiente de la recta.
La pendiente es la inclinación con respecto al eje X (eje de abscisas). Si m es
positiva (m > 0), entonces la función es creciente. En cambio, si la m es
negativa (m < 0), entonces la función es decreciente.
La pendiente m significa que si aumentamos la x
en una unidad, la y aumenta en m unidades. Si la m es positiva, según aumente
la x la y también irá aumentando (función creciente). En cambio, si m es
negativa, cuando aumenta la x la y disminuirá (función decreciente).
Función Cuadrática
Una función cuadrática es aquella
que puede escribirse como una ecuación de la forma:
f(x) = ax 2 + bx + c
donde a , b y c (llamados términos ) son números
reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero,
pero no igual que cero). El valor de b y de c sí puede ser cero
En la ecuación cuadrática cada
uno de sus términos tiene un nombre.
Así
ax 2 es el término cuadrático
bx es el término lineal
c es el término independiente
Cuando estudiamos la ecuación de
segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se
dice que es una ecuación completa , si a la ecuación le falta el término lineal
o el independiente se dice que la ecuación es incompleta
Representación gráfica de una
función cuadrática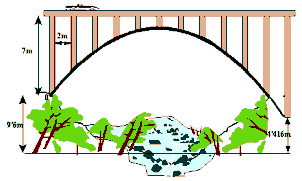
Dicha parábola tendrá algunas
características o elementos bien definidos dependiendo de los valores de la
ecuación que la generan.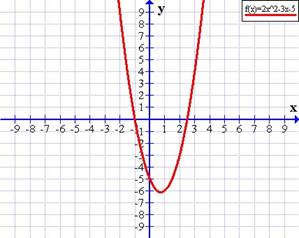
Si a < 0 (negativo) la parábola es convexa o
con puntas hacia abajo, como en
f(x) = −3x 2 + 2x + 3
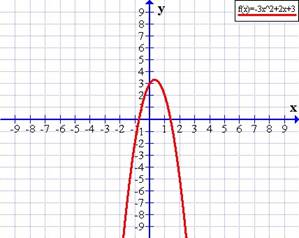


Además, cuanto mayor sea |a| (el
valor absoluto de a), más cerrada es la parábola
Puntos de corte en el eje de las
abscisas (Raíces o soluciones) (eje de las X)
Otra característica o elemento
fundamental para graficar una función cuadrática la da el valor o los valores
que adquiera x , los cuales deben calcularse.
Ahora, para calcular las raíces
(soluciones) de cualquier función cuadrática calculamos
f (x) = 0 .
Esto significa que las raíces
(soluciones) de una función cuadrática son aquellos valores de x para los cuales la expresión vale 0; es
decir, los valores de x tales que y = 0 ; que es lo mismo que f(x) = 0 .
Entonces hacemos
ax² + bx +c = 0
Como la ecuación ax² + bx +c = 0
posee un término de segundo grado, otro de primer grado y un término constante,
no podemos aplicar las propiedades de las ecuaciones, entonces, para resolverla
usamos la fórmula:
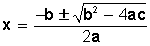
Entonces, las raíces o soluciones
de la ecuación cuadrática nos indican los puntos de intersección de la parábola
con el eje de las X (abscisas) .
Respecto a esta intersección, se
pueden dar tres casos:
Que corte al eje X en dos puntos
distintos
Que corte al eje X en un solo
punto (es tangente al eje x)
Que no corte al eje X
Eje de simetría o simetría
Otra característica o elemento de
la parábola es su eje de simetría .
El eje de simetría de una
parábola es una recta vertical que divide simétricamente a la curva; es decir,
intuitivamente la separa en dos partes congruentes. Se puede imaginar como un
espejo que refleja la mitad de la parábola.
Su ecuación está dada por:
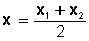
Donde x 1 y x 2 son las raíces de
la ecuación de segundo grado en x , asociada a la parábola.
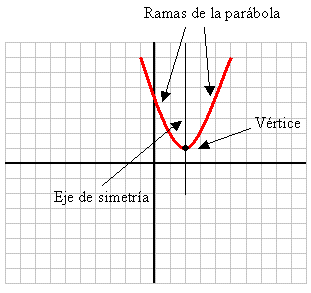
Como podemos ver en gráfico
precedente, el vértice de la parábola es el punto de corte (o punto de
intersección) del eje de simetría con la parábola y tiene como coordenadas
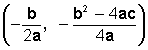
La abscisa de este punto
corresponde al valor del eje de simetría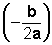
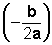
y la ordenada corresponde al valor
máximo o mínimo de la función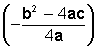
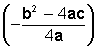
Según sea la orientación de la
parábola (recuerde el discriminante )
Función Cúbica
Una función cúbica (o función de
tercer grado) es una función polinómica de grado 3, es decir, que el mayor
exponente del polinomio es x elevado a 3 (x3):

La representación gráfica de la función cúbica es:

Una función cúbica puede tener
tres, dos o una raíz. Las raíces de una función son los elementos del dominio
tal que su imagen es nula (f(x) = 0).

Características de la función cúbica
Siendo f(x) = ax3+bx2+cx+d, entonces tenemos que:
- Dominio:

- Codominio:

- Derivada de la función cúbica:

- Integral de la función cúbica, es:

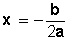

Comentarios
Publicar un comentario